Giải hệ phương trình bậc nhất 2 ẩn nhanh và chính xác

Bài viết dưới đây sẽ tổng hợp lại 2 cách giải hệ phương trình bậc nhất 2 ẩn nhanh và chính xác là phương pháp thế và phương pháp cộng đại số, mời các bạn tham khảo.

Hệ phương trình bậc nhất hai ẩn là gì?

Hệ phương trình bậc nhất hai ẩn là hệ phương trình có dạng

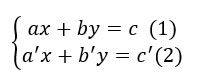
trong đó a, b, a’, b’, c, c’ là các số thực cho trước (a² + b² ≠ 0 và a’² + b’² ≠ 0) và x, y là ẩn.

Nếu hai phương trình (1) và (2) có nghiệm chung thì đó là nghiệm của hệ phương trình.

Giải hệ phương trình là tìm tất cả các nghiệm của nó.

Hai hệ phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.

Cách giải hệ phương trình bậc nhất 2 ẩn

Giải hệ phương trình bằng phương pháp thế

Bước 1: Từ một phương trình, ta rút 1 ẩn theo ẩn kia rồi thế vào phương trình thứ hai và rút gọn để được một phương trình mới còn 1 ẩn.

Bước 2: Giải phương trình mới rồi thế vào 1 phương trình ban đầu đầu để giải ra ẩn còn lại. Sau khi tính ra hai ẩn, ta kết luận nghiệm của hệ phương trình.

Chú ý:

• Để có lời giải đơn giản, ta thường chọn các phương trình có hệ số không quá lớn (bằng 1 hoặc -1) và biểu diễn ẩn có hệ số nhỏ hơn qua ẩn còn lại.
• Thay một phương trình trong hệ bởi phương trình một ẩn vừa tìm ta được hệ phương trình mới tương đương với hệ phương trình đã cho.

ví dụ 1: Giải hệ phương trình bậc nhất 2 ẩn sau:

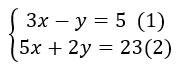
Giải:

Ví dụ 2: 

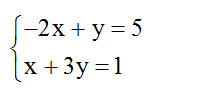
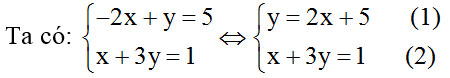
Thế (1) vào (2) ta được: x + 3(2x + 5) = 1

⇔ x + 6x + 15 = 1

⇔ 7x = -14

⇔ x = -2

Thay x = -2 vào (1) ta được y = 2.(-2) + 5 = 1

Vậy hệ phương trình có nghiệm duy nhất (-2;1)

Giải hệ phương trình bằng phương pháp cộng đại số

Các bước giải hệ phương trình bằng phương pháp cộng đại số:

Bước 1: Nhân hai vế của mỗi phương trình với một số thích hợp nếu cần sao cho các hệ số của một ẩn nào đó trong hai phương trình bằng nhau hoặc đối nhau.

Bước 2: Cộng hay trừ từng vế của hai phương trình của hệ đã cho để được một phương trình mới chỉ còn 1 ẩn.

Bước 3: Giải phương trình mới thu được ra 1 ẩn rồi thay vào 1 phương trình ban đầu để giải ẩn còn lại. Kết luận nghiệm của hệ phương trình đã cho.

Ví dụ 1: 

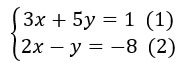
Giải: Để tạo ra hệ số của 1 ẩn trong hai phương trình bằng nhau hoặc đối nhau, ta chọn nhân 5 vào phương trình (2) thì sẽ có hệ số mới của y ở (2) là đối với hệ số của y ở (1):

5.2x – 5y = 5. (-8) hay

10x – 5y = – 40

Như vậy ta có hệ:

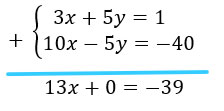
Cộng vế với vế của hai phương trình ta sẽ triệt tiêu được một nghiệm y.

Ta có phương trình mới chỉ còn nghiệm x là:

13x = – 39

suy ra x = -39/13 = -3.

Thay x = – 3 vào phương trình (1) ta có:

3.(-3) + 5y = 1

=> 5y = 10

suy ra y = 2.

Vậy nghiệm hệ phương trình đã cho là (x, y) = (-3, 2).

• Cách giải phương trình bậc 2