Tổng hợp các công thức lượng giác đầy đủ nhất dùng trong cả chương trình toán lớp 9, 10, 11, bao gồm các công thức lượng giác cơ bản, công thức nhân, biến đổi tích thành cổng, lượng giác của các cung đặc biệt, giá trị lượng giác của các góc đặc biệt, các công thức nghiệm cơ bản… Hãy nắm vững những công thức này để có thể triển khai các dạng bài tập về lượng giác. Mời các bạn tham khảo.
11 Công thức lượng giác phải nắm chắc
Khái niệm tỉ số lượng giác của một góc nhọn
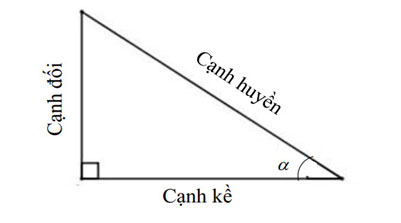
Với:
- sin α: là tỉ số giữa cạnh đối và cạnh huyền của góc α
- cos α: là tỉ số giữa cạnh kề và cạnh huyền của góc α
- tan α: là tỉ số giữa cạnh đối và cạnh kề của góc α
- cot α: là tỉ số giữa cạnh kề và cạnh đối của góc α
Mẹo học thuộc : Sin đi học, Cos không hư, Tan đoàn kết, Cot kết đoàn
Công thức chuyển đổi góc sang radian và ngược lại
Công thức lượng giác cơ bản
với
với
Công thức cộng lượng giác
1. sin (a ± b) = sin a.cos b ± cos a.sin b
2. cos (a + b) = cos a.cos b – sin a.sin b
3. cos (a – b) = cos a.cos b + sin a.sin b
Mẹo nhớ công thức cộng: Sin thì sin cos cos sin, cos thì cos cos sin sin dấu trừ. Tan thì tan nọ tan kia chia cho mẫu số 1 trừ tan tan.
Công thức các cung liên kết trên đường tròn lượng giác
Mẹo nhớ: cos đối, sin bù, phụ chéo, tan hơn kém π
Với mọi góc lượng giác α và số nguyên k ta có:
Hai góc đối nhau:
- cos (-x) = cos x
- sin (-x) = -sin x
- tan (-x) = -tan x
- cot (-x) = -cot x
Hai góc bù nhau:
- sin (π – x) = sin x
- cos (π – x) = -cos x
- tan (π – x) = -tan x
- cot (π – x) = -cot x
Hai góc phụ nhau:
- sin (π/2 – x) = cos x
- cos (π/2 – x) = sin x
- tan (π/2 – x) = cot x
- cot (π/2 – x) = tan x
Hai góc hơn kém π:
- sin (π + x) = -sin x
- cos (π + x) = -cos x
- tan (π + x) = tan x
- cot (π + x) = cot x
Hai góc hơn kém π/2:
- sin (π/2 + x) = cos x
- cos (π/2 + x) = -sin x
- tan (π/2 + x) = -cot x
- cot (π/2 + x) = -tan x
Công thức nhân đôi
Công thức nhân đôi
- sin2a = 2sina.cosa
- cos2a = cos2a – sin2a = 2cos2a – 1 = 1 – 2sin2a
Công thức nhân ba
- sin3a = 3sina – 4sin3a
- cos3a = 4cos3a – 3cosa
Công thức nhân bốn
- sin4a = 4.sina.cos3a – 4.cosa.sin3a
- cos4a = 8.cos4a – 8.cos2a + 1 hoặc cos4a = 8.sin4a – 8.sin2a + 1
Công thức hạ bậc
Thực ra những công thức này đều được biến đổi ra từ công thức lượng giác cơ bản, ví dụ như: sin2a=1 – cos2a = 1 – (cos2a + 1)/2 = (1 – cos2a)/2.
Công thức biến đổi tổng thành tích
Mẹo nhớ: cos cộng cos bằng 2 cos cos, cos trừ cos bằng trừ 2 sin sin; sin cộng sin bằng 2 sin cos, sin trừ sin bằng 2 cos sin.
Công thức biến đổi tích thành tổng
Phương trình lượng giác
Phương trình lượng giác cơ bản
3. tan a = tan b ⇔ a = b + kπ; (k ∈ Z)
4. cot a = cot b ⇔ a = b + kπ; (k ∈ Z)
Phương trình lượng giác đặc biệt
Dấu của các giá trị lượng giác
| Góc phần tư số | I | II | III | IV |
| Giá trị lượng giác | ||||
| sin x | + | + | – | – |
| cos x | + | – | – | + |
| tan x | + | – | + | – |
| cot x | + | – | + | – |
Bảng giá trị lượng giác một số góc đặc biệt
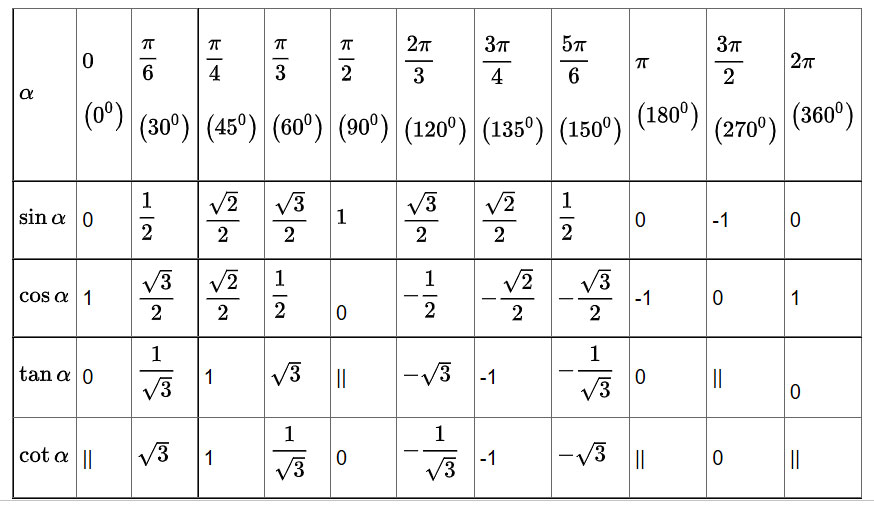
Quan sát trực quan các góc đặc biệt trên đường tròn lượng giác như sau:

Tỉ số lượng giác của 2 góc phụ nhau. (α + β = 90°)
| sin α = cos β | cos α = sin β |
| tan α = cot β |
cot α = tan β |
Công thức lượng giác bổ sung
Biểu diễn công thức theo
Các công thức đạo hàm và đạo hàm lượng giác đầy đủ nhất