Cấp số cộng là gì? Công thức cấp số cộng như thế nào? Mời các bạn cùng tìm hiểu bài viết dưới đây để tìm hiểu lý thuyết về cấp số cộng và tham khảo một số ví dụ chi tiết về công thức tính cấp số cộng nhé.
Mục lục bài viết
- Cấp số cộng là gì?
- Công thức tính cấp số cộng
- Ví dụ về cấp số cộng
- Phương pháp giải cấp số cộng
- Ví dụ về cấp số cộng

Cấp số cộng là gì?
Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.
Số d được gọi là công sai của cấp số cộng.
Nếu (un) là cấp số cộng với công sai d, ta có công thức truy hồi
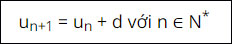
Đặc biệt khi d = 0 thì cấp số cộng là một dãy số không đổi (tất cả các số hạng đều bằng nhau).
Công thức tính cấp số cộng
1. Số hạng tổng quát của cấp số cộng
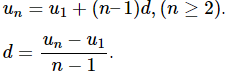
2. Công thức tính tổng n số hạng đầu (tổng riêng thứ n) thông qua số hạng đầu và công sai
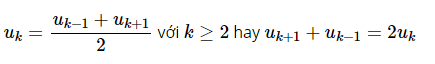
3. Công thức liên hệ với hai số hạng liền kề
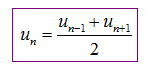
4. Công thức liên hệ giữa hai số hạng bất kỳ
![]()
Ví dụ về cấp số cộng
Phương pháp giải cấp số cộng
Để xác định một cấp số cộng, ta cần xác định số hạng đầu và công sai. Do đó, ta thường biểu diễn giả thiết của bài toán qua u1 và d.
Cho cấp số cộng (un). Khi đó:
un= u1+ (n-1)d: số hạng tổng quát của cấp số cộng;
d: công sai của cấp số cộng

Ví dụ về cấp số cộng
Ví dụ 1: Tìm bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120.
Giải: Giả sử bốn số hạng đó là a – 3x, a – x, a + x, a + 3x với công sai là d = 2x. Khi đó, ta có:

Vậy bốn số cần tìm là 2,4,6,8.
Ví dụ 2:
Cho cấp số cộng
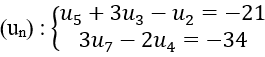
1. Tính số hạng thứ 100 của cấp số ;
2. Tính tổng 15 số hạng đầu của cấp số ;
3. Tính S = u4 + u5 + …+ u30.
Giải:
Từ giả thiết bài toán, ta có:
1. Số hạng thứ 100 của cấp số: u_100 = u_1+ 99d = -295
2. Tổng của 15 số hạng đầu:
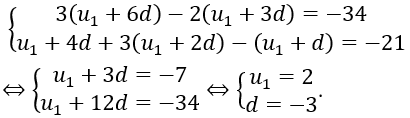
3. Ta có:
![]()